Sistemas Numéricos - Octal
O sistema octal é um sistema de numeração de base 8, ou seja, recorre a 8 símbolos (0,1,2,3,4,5,6,7) para a representação de um determinado valor. O sistema octal foi muito utilizado no mundo da computação, como uma alternativa mais compacta do sistema binário, na programação em linguagem de máquina. Atualmente, o sistema hexadecimal é um dos mais utilizado como alternativa viável ao sistema binário.
História
O sistema octal tem sua origem na antiguidade, quando as pessoas usavam as mãos para contar os animais oito a oito. Por exemplo, para contar o número de vacas em um estábulo, uma começou a contar com a mão direita, unindo o polegar com o dedo mindinho; depois, para contar o segundo animal, o polegar foi unido ao dedo indicador, e assim por diante, com os dedos restantes de cada mão, até completar 8.
Existe a possibilidade de que, nos tempos antigos, o sistema de numeração octal fosse usado antes do decimal para poder contar os espaços interdigitais; isto é, conte todos os dedos, exceto os polegares.
Posteriormente, o sistema de numeração octal foi estabelecido, originado do sistema binário, porque ele precisa de muitos dígitos para representar apenas um número; depois disso, os sistemas octano e hexagonal foram criados, os quais não requerem tantos dígitos e podem ser facilmente convertidos para o sistema binário.
Como funciona o sistema octal
O sistema octal consiste em oito dígitos que variam de 0 a 7. Eles têm o mesmo valor que no caso do sistema decimal, mas seu valor relativo muda dependendo da posição que ocupam. O valor de cada posição é dado pelos poderes básicos 8.
As posições dos dígitos em um número octal têm os seguintes pesos:
8^4 , 8^3 , 8^2 , 8^1 , 8^0 , ponto octal 8^-1 8^-2 , 8^-3 8^-4 , 8^-5 .
O principal dígito octal é 7; Dessa forma, ao contar neste sistema, uma posição de um dígito é aumentada de 0 para 7. Quando atinge 7, é reciclado para 0 na próxima contagem; Dessa forma, a próxima posição do dígito é aumentada. Por exemplo, para contar sequências, no sistema octal será:
- 0, 1, 2, 3, 4, 5, 6, 7, 10.
- 53, 54, 55, 56, 57, 60.
- 375, 376, 377, 400.
Existe um teorema fundamental que é aplicado ao sistema octal e é expresso da seguinte maneira:
Nesta expressão, di representa o dígito multiplicado pela potência base 8, que indica o valor posicional de cada dígito, da mesma forma como é ordenado no sistema decimal.
Por exemplo, você tem o número 543.2. Para levá-lo ao sistema octal, ele se decompõe da seguinte forma:
N = ∑ [(5 * 8^2 ) + (4 * 8^1 ) + (3 * 8^0 ) + (2 * 8 ^(-1 ))] = (5 * 64) + (4 * 8) + (2 * 1 ) + (2 * 0,125)
N = 320 +32 + 2 + 0,25 = 354 + 0,25 d
Dessa forma você tem que 543,2 q = 354,25 d . O subscrito q indica que é um número octal que também pode ser representado pelo número 8; e o subscrito d refere-se ao número decimal, que também pode ser representado pelo número 10.
Conversão do sistema octal para decimal
Para converter um número do sistema octal para seu equivalente no sistema decimal, basta multiplicar cada dígito octal pelo seu valor posicional, começando pela direita.
Exemplo 1
732 #8 = (7 * 8 2 ) + (3 * 8 1 ) + (2 * 8 0 ) = (7 * 64) + (3 * 8) + (2 * 1)
732 #8 = 448 +24 +2
732 #8 = 474 10
Exemplo 2
26,9 #8 = (2 * 8 1 ) + (6 * 8 0 ) + (9 * 8 -1 ) = (2 * 8) + (6 * 1) + (9 * 0,125)
26,9 #8 = 16 + 6 + 1,125
26,9 #8 = 23,125 10
Referências
- Bressan, AE (1995). Introdução aos sistemas de numeração. Universidade Argentina da Companhia.
- Harris, JN (1957). Introdução aos Sistemas de Numeração Binários e Octais: Lexington, Massachusetts. Agência de Informações Técnicas de Serviços Armados.
- Kumar, AA (2016). Fundamentos de Circuitos Digitais. Aprendizagem Pvt.
- Peris, XC (2009). Sistemas Operacionais Monopod.
- Ronald J. Tocci, NS (2003). Sistemas digitais: princípios e aplicações. Educação Pearson.
Fontes:

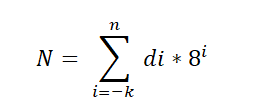



Comentários
Postar um comentário